液壓頂升平橋梁柱構件的位移計算研究

       簡述：

1)有風載荷作用時，立柱頂端最大偏移量δw=720mm，大約為立柱高度矗的1.41%；

2)無風載荷作用時，立柱頂端最大偏移量δc=472mm，大約為立柱高度矗的0.92%；

3)立柱頂端偏移量艿。與力矩嵫呈線性正比關系；隨著力矩的增大，偏移量也隨之增大；

4)立柱頂端偏移量艿。與軸向力Q呈非線性關系；隨著軸向力的增大，偏移量也隨之增大。

為保證液壓頂升平橋平穩工作，建議采取附著技術，方可保證安全施工。

1、引言

液壓頂升平橋…廣泛用于冷卻塔施工，最低高度達50多m:液壓頂升平橋的立柱（或塔身）是關鍵的結構件，其撓度既影響整機強度，又影響其穩定性。立柱在不平衡的自重、活動荷重、風載荷與動載荷作用下會彎曲，產生更大的變形，使彎矩增大。因此如何正確計算液壓頂升平橋頂部的最大變形位移，是保證安全施工的重要因素，也是采取有關措施的依據。

2、梁一柱的撓度曲線

2.1有風載荷時梁一柱的撓度曲線

立柱的彈性變形是白于載荷偏心造成的。如在有風狀態下，繞起重機中心線的凈力矩Me，軸向力Q；風載荷：認為回轉部以上受風面積的風力W為集中力并作用在回轉部，高出冷卻塔部分的立柱風載荷為w，高出冷卻塔部分（與坐標原點距離，可視為定值）的長度為x1。液壓頂升平橋的彈性變形計算模型如圖1所示。

假設條件：①平橋2、塔機3及基礎5均視為剛性體；②立柱1視為彈性體并為等截面。

立柱的力學表現類似懸臂梁，屬于梁一柱構件。根據彈性穩定原理，其基本表達式為:

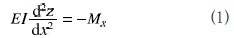
頂端的力矩為：

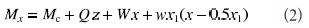
故撓度曲線為：

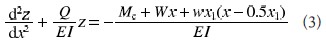
令k2=Q/E1，計算得

相對于基座，即立柱固定端的最大偏移量z(h)=δw。，則

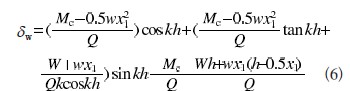
2.2無風載荷時梁一柱的撓度曲線

如在無風狀態下，繞起重機中心線的凈力矩Mc，軸向力Q。頂端的力矩為

故撓度曲線為

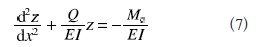
仍令k2=Q/EI，得梁一柱構件任意一點的彈性偏移量計算式為

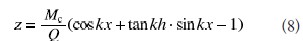
相對于基座，即立柱固定端的最大偏移量z(h)=δc。，則

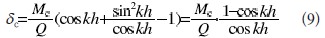
2.3實例計算

YDQ型25.6tm液壓頂升平橋工作時，其載荷為頂端不平衡力矩Mc=789.55kNm，承受軸向力Q=172.64kN，橋身均布風載荷為w=0.3696kN／m，水平風力W=12.62kN;平橋的高度h=51.15m，平橋頂端距冷卻塔頂部的距離x1=14.15m;彈性模量E=200GPa，立柱慣性矩/=1.33×10-2IT14，水平靜位移AL≤1.34h／100，求其頂端的偏移量。

中間參量計算得：k=8.1×10^-3m^-1，sinkh=0.4026.coskh=0.9154.tankh=0.4398.

1)育風條件下頂部的最大偏移量aw若在有風條件下，將已知參數和上述計算結果代人方程(5)中，可求得頂部的最大偏移量aw-0.7194m>[A/]=1.34h／100=0.6905m.

2)無風條件下頂部的最大偏移量δc。若在無風條件下，將已知參數和相關計算結果代入方程(9)中，可求得最大偏移量δc=0.4718m。

由上述計算可以得出：有風載荷作用時，立柱頂端最大偏移量δw。大約為立柱高度h的1.41%；無風載荷作用時，立柱頂端最大偏移量δc。大約為立柱高度h的0.92%。

3)有風條件下最大偏移量δw與Mc的關系由式(5)可知

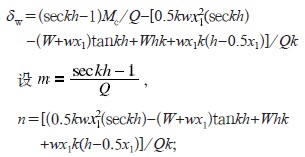
如k、h、Q、w、X1均為常量，則m、n為常量；δw=mMc+n。

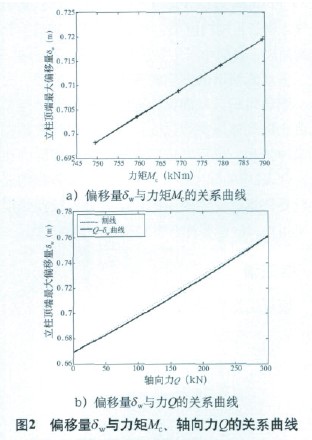
由此可見，δw與Mc呈線性正比關系，如圖2a所示。

4)有風條件下最大偏移量δw與Q昀關系由式(5)可知

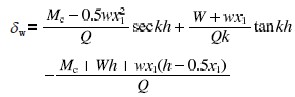
從上式可以得出：δw與Q為非線性關系，如圖2（b）所示。